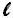TRAPÉZIO
A área do trapézio está relacionada com a área do triângulo que é calculada utilizando a seguinte fórmula: A =
b . h (b = base e h = altura).
2
Observe o desenho de um trapézio e os seus elementos mais
importantes (elementos utilizados no
cálculo da sua área):
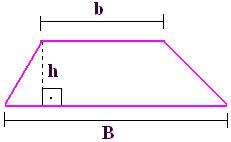
Um trapézio é formado por uma base maior (B), por uma base menor (b) e por uma altura (h).
Para fazermos o
cálculo da área do trapézio é preciso dividi-lo em dois triângulos, veja como:
Primeiro: completamos as alturas no trapézio:
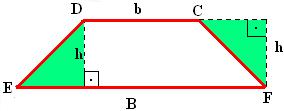
Segundo: o dividimos em dois triângulos:
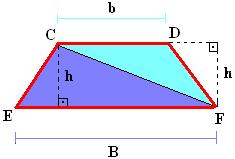
A área desse trapézio pode ser calculada somando as áreas dos dois triângulos (∆CFD e ∆CEF).
Antes de fazer o
cálculo da área de cada triângulo separadamente observamos que eles possuem bases diferentes e alturas iguais.
Cálculo da área do ∆CEF:
A∆1 =
B . h
2
Cálculo da área do ∆CFD:
A∆2 =
b . h
2
Somando as duas áreas encontradas, teremos o cálculo da área de um trapézio qualquer:
AT = A∆1 + A∆2
AT =
B . h +
b . h
2 2
AT =
B . h + b . h →
colocar a altura (h) em evidência, pois é um termo comum aos dois fatores.
2
AT =
h (B + b)
2
Portanto, no cálculo da área de um trapézio qualquer utilizamos a seguinte fórmula:
A = h (B + b)
2
h = altura
B = base maior do trapézio
b = base menor do trapézio
Losango
Um losango é formado por dois triângulos idênticos, com base igual a d (diagonal menor) e altura igual a D / 2 (metade da diagonal maior).

Os triângulos ABC e ACD são iguais, portanto as suas superfícies (áreas) também são iguais. Veja o
cálculo:
Cálculo da área do triângulo ABC e BCD.
A fórmula que utilizamos para o
cálculo da área de um triângulo é

, b de base e h de altura, substituindo os dados do losango na fórmula temos:
Base = d (diagonal menor)
Altura = D/2 (metade da diagonal maior)
Assim, a área dos triângulos será:
A = d . D
2
2
Como a área de um losango é a soma das áreas dos triângulos ABC e ACD, concluímos que a área do losango será:
AL = A
ABC + A
BCD

Portanto, a área do losango poderá ser calculada utilizando a seguinte fórmula:
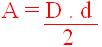
Retângulo
Podemos concluir que a área de qualquer retângulo é:
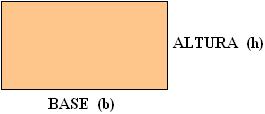 A = b . h
Quadrado
A = b . h
Quadrado
É um tipo de retângulo específico, pois tem todos os lados iguais. Sua área também é calculada com o
produto da base pela altura. Mas podemos resumir essa fórmula:
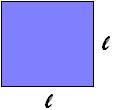
Como todos os lados são iguais, podemos dizer que base é igual a

e a altura igual a
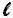
, então, substituindo na fórmula A = b . h, temos:
A =
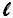
.